Motions occur everywhere in our lives. Let say you are buying something in the supermarket, you are pushing a cart and you want to put the goods into the cart for the payment at the cashier.
How do you describe the motion?
Moving? Stopped?
Fast? Slow? It is too subjective.
Let me do some mathematical description for that.
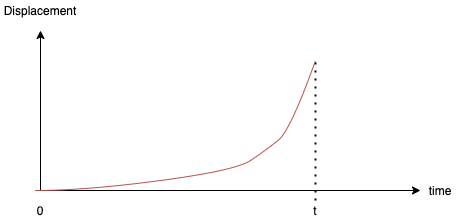
Considering a 1-Dimensional movement, when a cart is moved from 1 point to another point for time t(in seconds). The displacement is from the original point changes as time goes towards t.
We may define the slope of the graph as the velocity.
We may also define the change of the slope as the acceleration.
In terms of the derivatives, we may write,
![\[ a=\frac{dv}{dt} \quad or \quad v=\int_{}{} a \,dt \]](https://www.ymleung.com/wp-content/ql-cache/quicklatex.com-58762f63095079112040a9a1d86c0d74_l3.png "Rendered by QuickLaTeX.com")
![\[ v=\frac{ds}{dt} \quad or \quad s=\int_{}{} v \,dt \]](https://www.ymleung.com/wp-content/ql-cache/quicklatex.com-9df68d3a8a2884b3397644aef5298e8f_l3.png "Rendered by QuickLaTeX.com")
where 
is velocity, 
is acceleration, and 
is displacement
Now, let say if the acceleration is a constant, then:
(1) 
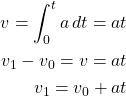
(2) 
where 
is initial velocity and 
is the final velocity
from equation 1 and 2, we may also derive that:
(3) 
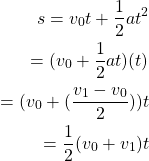
(4) 
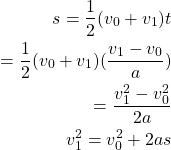
The above equations are to describe the motion when the acceleration is constant.
But of course, it is impossible to happen in the real life.